Decreasing suicide risk with math
Suicide is a common reality, accounting for approximately 800,000 deaths per year worldwide.1 Properly assessing and minimizing suicide risk can be challenging. We are taught that lithium and clozapine can decrease suicidality, and many psychiatrists prescribe these medications with the firm, “evidence-based” belief that doing so reduces suicide risk. Paradoxically, what they in fact might be doing is the exact opposite; they may be giving high-risk patients the opportunity and the means to attempt suicide with a lethal amount of medication.
One patient diagnosed with a mood disorder who attempted suicide had a surprising point of view. After taking a large qu
Operations research is a subfield of mathematics that tries to optimize one or more variables when multiple variables are in play. One example would be to maximize profit while minimizing cost. During World War II, operations research was used to decrease the number of munitions used to shoot down airplanes, and to sink submarines more efficiently.
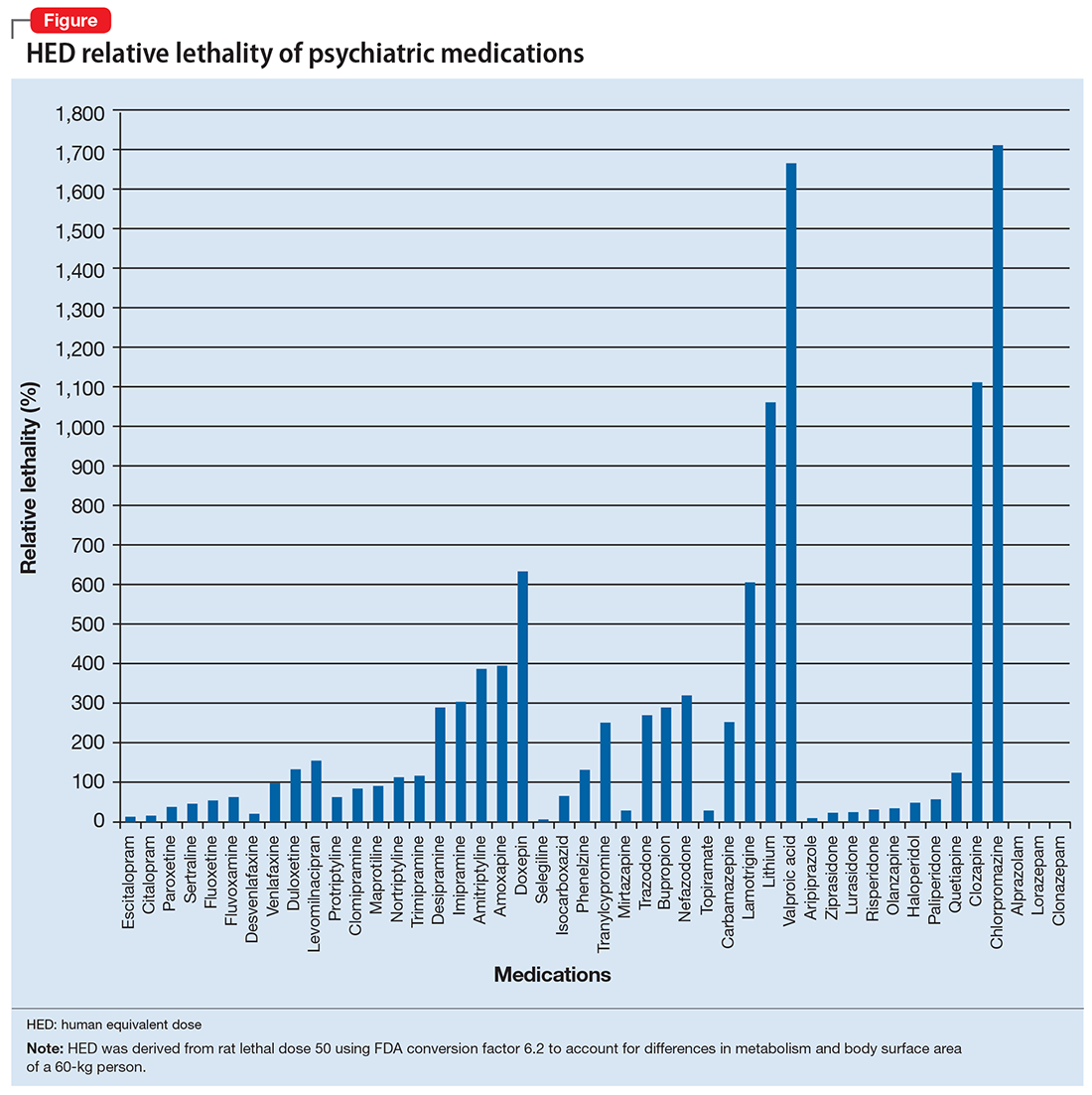
Focusing on the patient who attempted suicide by overdose, the question was: If she was discharged from the psychiatry unit with a 30-day supply of medication, how lethal would that prescription be if deliberately taken all at once? And what can be done to minimize this suicide risk? Psychiatrists know that some medications are more dangerous than others, but few have performed quantitative analysis to determine the potential lethality of these medications. The math analysis did not involve multivariable calculus or differential equations, only multiplication and division. The results were eye-opening.
Calculating relative lethality
The lethal dose 50 (LD50) is the dose of a medication expressed in mg/kg that results in the death of 50% of the animals (usually rats) used in a controlled experiment. Open-source data for the LD50 of medications is provided by the manufacturers.
I tabulated this data for a wide range of psychiatric medications, including antipsychotics, mood stabilizers, and selective serotonin reuptake inhibitors, in a spreadsheet with columns for maximum daily dose, 30-day supply of the medication, LD50 in mg/kg, LD50 for a 60-kg subject, and percentage of the 30-day supply compared with LD50. I then sorted this data by relative lethality (for my complete data, see Figure 1 and the Table).
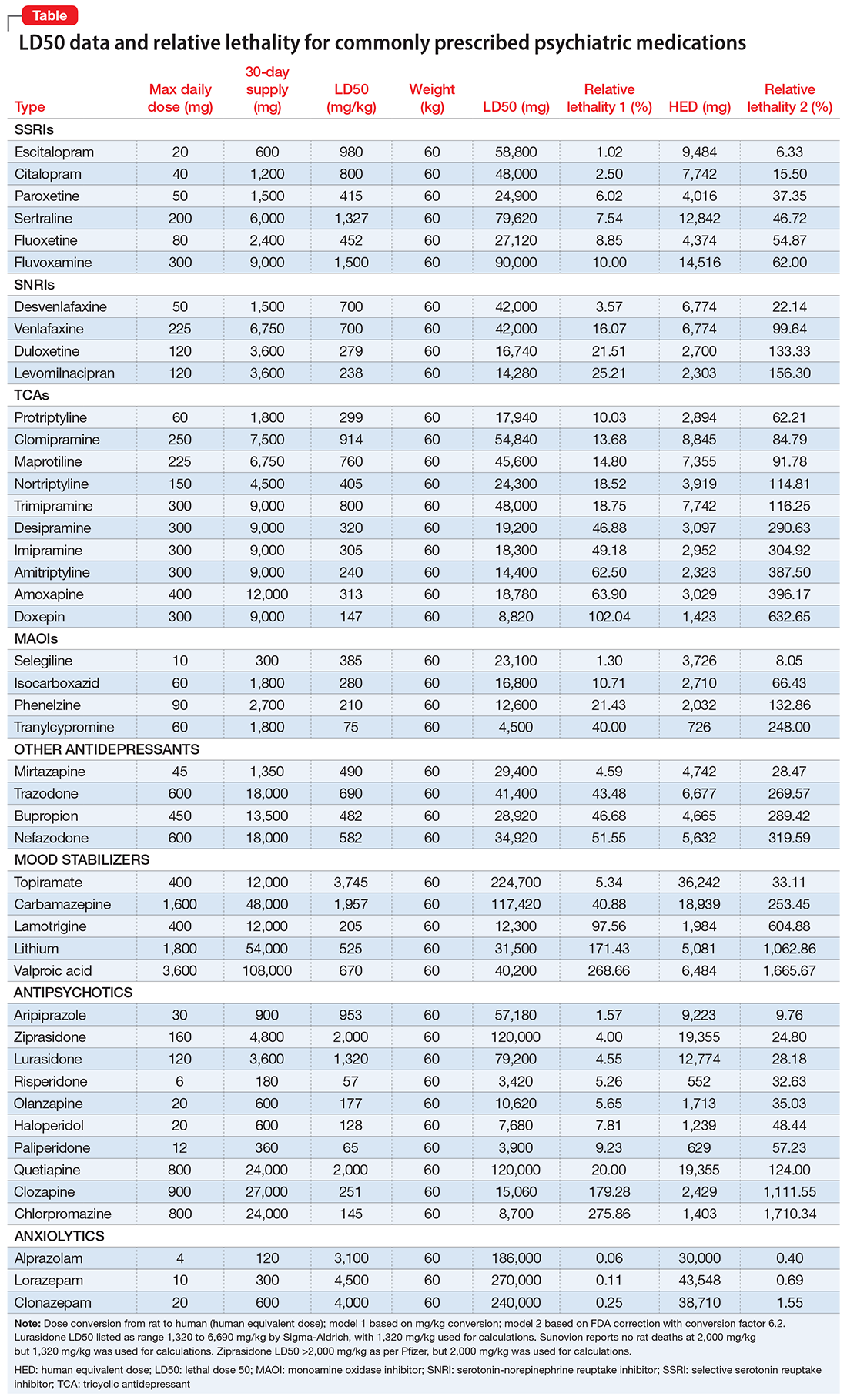
The rat dose in mg/kg was extrapolated to the human equivalent dose (HED) in mg/kg using a conversion factor of 6.2 (for a person who weighs 60 kg, the HED = LD50/6.2) as suggested by the FDA.2 The dose for the first fatality is smaller than the HED, and toxicity occurs at even smaller doses. After simplifying all the terms, the formula for the HED-relative lethality is f(x) = 310x/LD50, where x is the daily dose of a medication prescribed for 30 days. This is the equation of a straight line with a slope inversely proportional to the LD50 of each medication and a y-axis intercept of 0. Each medication line shows that any dose rising above 100% on the y-axis is a quantum higher than the lethal dose.