Chi-square and Fisher’s exact tests
This article aims to introduce the statistical methodology behind chi-square and Fisher’s exact tests, which are commonly used in medical research to assess associations between categorical variables. This discussion will use data from a study by Mrozek1 in patients with acute respiratory distress syndrome (ARDS). This was a multicenter, prospective, observational study: multicenter because it included data from 10 intensive care units, prospective because the study collected the data moving forward in time, and observational because the study investigators did not have control over the group assignments but rather used the naturally occurring groups. The study objective was to characterize focal and nonfocal patterns of lung computed tomography (CT)-based imaging with plasma markers of lung injury.
The primary grouping variable was type of ARDS (focal vs nonfocal) as determined by CT scans and other lung imaging tools. In this study, there were 32 (27%) patients with focal ARDS and 87 (73%) patients with nonfocal ARDS. What will be important, however, is classifying the type of variables because this determines the type of analyses performed. Type of ARDS is a categorical variable with 2 levels.
The primary study endpoint was plasma levels of the soluble form of the receptor for advanced glycation end product. There were also a number of secondary study endpoints that can be grouped as either patient outcomes or biomarkers. Patient outcomes included the duration of mechanical ventilation and both 28- and 90-day mortality. Levels of other biomarkers included surfactant protein D, soluble intercellular adhesion molecule-1, and plasminogen activator inhibitor-1.
This article focused on the secondary outcome of 90-day mortality beginning at disease onset. Again, we are interested in classifying this variable, which is categorical with 2 levels (yes vs no). So the scenario is that we want to assess the relationship between the type of ARDS (focal vs nonfocal) and 90-day mortality (yes vs no). In its most basic form, this scenario is an investigation into the association among 2 categorical variables.
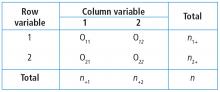
When there are 2 categorical variables, the data can be arranged in what is called a contingency table (Figure 1). Because both variables are binary (2 levels), it is called a 2 × 2 table. However, a contingency table can be generated for 2 categorical variables with any number of levels—in that case, it is called an r ×c table, where r is the number of levels for the row variable and c is the number of levels for the column variable. The actual raw counts or frequencies are recorded inside the table cells. The cell counts are often referred to as observed counts and thus the notation (Oij) is used. The subscript i identifies the specific level of the row variable, and in this example it can equal 1 or 2 since the row variable is binary. Similarly, the subscript j identifies the specific level of the column variable and in this example it can equal 1 or 2 since the column variable is binary. Therefore, O11 represents the number of patients who have the row variable = level 1 and the column variable = level 1.
In addition to the row and column variable cells, there are also the margin totals. These totals are either the row margin total (summing across the row) or the column margin total (summing down the column). For example, n1+ is the sum of the row where the row variable equal 1 (O11 + O12 = n1+). Finally, at the very bottom right corner is the grand total, which equals the sample size.
The goal is to test whether or not these 2 categorical variables are associated with each other. The null hypothesis (Ho) is that there is no association between these 2 categorical variables and the alternative hypotheses (Ha) is that there is an association between these 2 categorical variables.
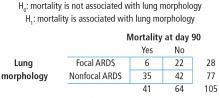
The next step is to translate the generic form of the hypotheses into hypotheses that are specific to the research question. In this case, the null hypothesis is that mortality is not associated with lung morphology and the alternative hypothesis is that mortality is associated with lung morphology.
The contingency table cells can be populated with the numbers found in the article. It has our outcome of focus—mortality at day 90—both the count and the percent. The results are broken down by type of ARDS (focal vs nonfocal) as follows:
- Focal ARDS = 6 patients (21.4%)
- Nonfocal ARDS = 35 patients (45.5%).
First, the row variable is lung morphology, and it has two levels (focal vs nonfocal). Next, the column variable is 90-day mortality and it has 2 levels (yes vs no). Finally, the table must be populated, but be careful not to assume that there are no missing data. Begin with the cell counts: there were 6 focal ARDS patients and 35 nonfocal ARDS patients who died within 90 days. These two numbers populate the first column and result in a column total of 41. Next, use the reported percentages to calculate the row totals. Six is 21.4% of 28, so the first row total is 28. Thirty-five is 45.5% of 77, so the second row total is 77. If there are 28 patients with focal ARDS and 77 with nonfocal ARDS, then the grand total is 28 + 77 = 105. The remaining values can be obtained by subtraction. If there are 105 total patients and 41 die within 90 days, then 105 − 41 = 64 patients who do not die within 90 days and this is the second column total. Similarly, if there are 28 focal ARDS patients and 6 die within 90 days, then 28 − 6 = 22 patients who do not die within 90 days. Lastly, if there are 77 nonfocal ARDS patients and 35 die within 90 days, then 77 − 35 = 42 patients who do not die within 90 days. Now the contingency table is complete.